Na první pohled se tato otázka zdá být jednoduchá, ale při bližším zkoumání odhaluje překvapivou složitost. Jednou z nejpřímějších metod měření rychlosti světla je použití zdroje světla, přesných hodin (chronometru), zrcadla a detektoru světla. Zdroj světla, chronometr a detektor jsou umístěny v bodě A, zatímco zrcadlo je umístěno v bodě B a odráží světlo zpět do bodu A (obr. 1).
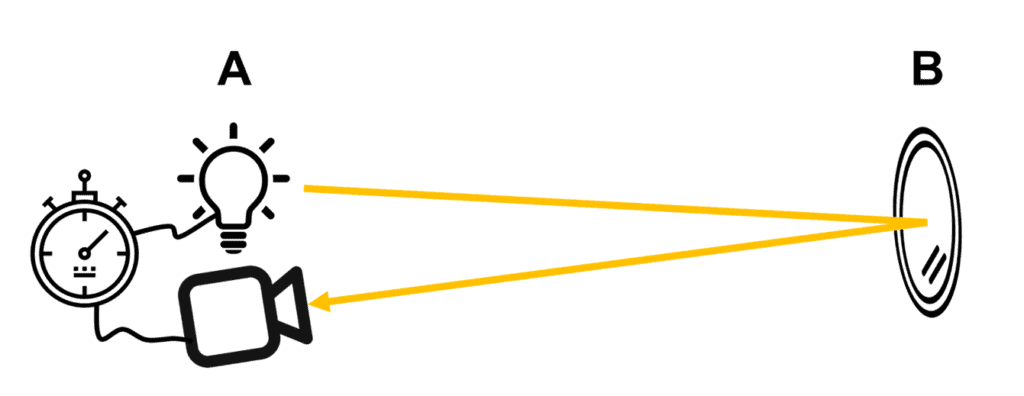
Obrázek 1
Musíme si na to posvítit
Experiment probíhá následovně: když se zapne zdroj světla, spustí se chronometr. Jakmile detektor zaznamená světlo vracející se z bodu B, zastaví chronometr. Rychlost světla se pak vypočítá jako dvojnásobek vzdálenosti mezi body A a B dělený zaznamenaným časem. Tato metoda měří průměrnou rychlost světla cestujícího z bodu A do bodu B a zpět do bodu A. Tyto metody jsou natolik přesné a konzistentní, že metr byl definován na základě rychlosti světla: světlo má rychlost 299 792 458 m/s a jeden metr je vzdálenost, kterou světlo urazí za přesně 1/299 792 458 sekundy [1].
Co když se však rychlost světla liší v jednotlivých směrech – je jiná při cestě k bodu B a jiná při cestě zpět k bodu A? Jednou z možností by bylo umístit detektor do bodu B a obejít tak potřebu zrcadla (obr. 2). Tato metoda však vyžaduje, aby detektor poslal zpět signál chronometru v bodě A v okamžiku, kdy zaznamená světlo. Protože tento signál se rovněž šíří rychlostí světla (nebo pomaleji), opět měříme průměrnou rychlost světla v obou směrech.

Obrázek 2
Seřídíme si hodiny
Další přístup spočívá v použití dvou synchronizovaných hodin. Nejprve jsou oboje hodiny synchronizovány v bodě A a poté jsou jedny z nich přesunuty do bodu B. Hodiny v bodě A zaznamenají čas vyslání světla t₁, zatímco hodiny v bodě B zaznamenají čas jeho přijetí t₂ (obr. 3). Rychlost světla pak lze vypočítat jako |AB|/(t₂−t₁), kde |AB| je vzdálenost mezi body A a B. Tento postup však komplikuje speciální teorie relativity. Podle ní se pohybující se hodiny opožďují v důsledku dilatace času. Protože hodiny v bodě B musely být přemístěny z bodu A, podléhají časové dilataci, což vede k podhodnocení rozdílu t₂−t₁. Můžeme se pokusit tento efekt opravit, ale závisí na rychlosti posunu hodin vůči rychlosti světla – tedy na samotné věci, kterou se snažíme změřit. Pokud je však rychlost světla cestou k zrcadlu jiná než cestou zpět, nemáme dostatek informací k určení správné korekce.

Obrázek 3
Mohl by tento problém vyřešit extrémně pomalý přesun hodin mezi body A a B, aby se minimalizovaly relativistické efekty? Překvapivě ani toto nepomůže. Pokud předpokládáme, že rychlost světla není v obou směrech stejná, lze ukázat, že hodiny přesunuté do bodu B budou vždy zpožděné nebo posunuté o určitý čas, bez ohledu na rychlost jejich pohybu. V důsledku toho by naměřená rychlost byla přesně stejná jako při použití zrcadla, tedy průměrná hodnota v obou směrech. Tato metoda tedy rovněž neodhalí žádný rozdíl v rychlosti světla v jednotlivých směrech [2].
Nevypadají náhodou galaxie v různých směrech různě staré?
A co astronomická pozorování? Pokud se vesmír jeví ve všech směrech stejný, neznamená to, že světlo se musí šířit stejnou rychlostí ve všech směrech? Na první pohled by se to mohlo zdát logické. Pokud by velký třesk nastal současně pro všechny galaxie, pak by rozdílná rychlost světla v různých směrech způsobila, že by galaxie na jedné straně kosmu vypadaly starší než ty na druhé. Ve skutečnosti by se však nic takového nestalo. Jakákoli změna rychlosti světla by byla doprovázena odpovídajícími změnami v dilataci času a prostoru, což by nakonec zachovalo jednotný vzhled vesmíru [3].
Až dosud nebyl navržen žádný vědecký experiment, který by byl citlivý na rozdíly v rychlosti světla v různých směrech. Měli bychom si s tím dělat starosti? Je to zásadní nedostatek v našem chápání fyziky?
Na jedné straně neexistuje žádný experiment, který by dokázal přímo změřit jednosměrnou rychlost světla: lze určit pouze tu průměrnou ve směru k bodu a zpět k pozorovateli. Na druhé straně moderní fyzika předpokládá, že rychlost světla je ve vakuu vždy stejná ve všech směrech, a tento předpoklad vedl k teoriím, které s velkou přesností popisují širokou škálu jevů od interakcí mezi subatomárními částicemi až po rozpínání vesmíru.
Jednodušší vysvětlení stačí
Princip Occamovy břitvy říká, že pokud jednodušší vysvětlení postačuje, není důvod přidávat zbytečnou složitost. Vzhledem k tomu, že fyzikální teorie fungují bez problémů za předpokladu, že rychlost světla je stejná ve všech směrech, vědci nevidí důvod komplikovat modely novými myšlenkami o šíření světla.
Pro Zeptej se vědce odpovídal Benoit
Zdroje:
[1] https://www.nist.gov/si-redefinition/meter
[2] https://doi.org/10.1016/S0370-1573(97)00051-3
[3] https://doi.org/10.1017/pasa.2021.2
Doporučené video (pouze anglicky): https://www.youtube.com/watch?v=pTn6Ewhb27k

