U všech tábornických rad a návodů je potřeba předem říct, že fungují přibližně a nelze je používat všeobecně. U této poučky je nutno vědět, že slunce se pohybuje od východu na západ a na severní polokouli se pohybuje hlavně po jižní straně oblohy. Pokud bychom použili tuto poučku během rovnodennosti, platila by dokonale celý den – pokud bychom zaznamenávali konec stínu vrhaný tyčkou a udělali spojnici, tato spojnice by ukazovala ze západu na východ. Je to z toho důvodu, že sluneční světlo během rovnodennosti dopadá kolmo na zemskou osu.
Mimo rovnodennost poučka není přesná, v časech blízkých východu a západu slunce selhává. Tato chyba bude největší během letního a zimního slunovratu. Existuje ale časové okno, kdy poučka bude platit v jakoukoliv roční dobu. Kolem pravého poledne se bude stín přesouvat ze západu na východ a jde tedy použít k určení západovýchodního směru. Pravé poledne je okamžik, kdy je Slunce na obloze nejvýše a v našich zeměpisných šířkách přesně na jihu. Tato doba se může od 12:00 na našich hodinkách lišit. Během letního času je v České republice pravé poledne až kolem 13:00, ale v jiných zemích může být rozdíl větší. Předpokládá se, že tuto poučku budete používat právě kolem poledne, protože během východu a západu slunce se dají zeměpisné strany určit poměrně snadno podle toho, kde slunce vychází nebo zapadá.
Pokud bychom chtěli zjistit jak moc přesná je poučka, nejlepší a nejpřesnější postup je spočítat si polohu stínu v různých časech a ideálně v různých dnech. Výpočet je detailně popsán v poslední části textu a k jeho pochopení je dobré kamarádit se s matematikou. Ale výsledek toho, jak se mění dráha stínu je na obrázku 1. Z toho je patrné, kdy a jak poučka funguje.
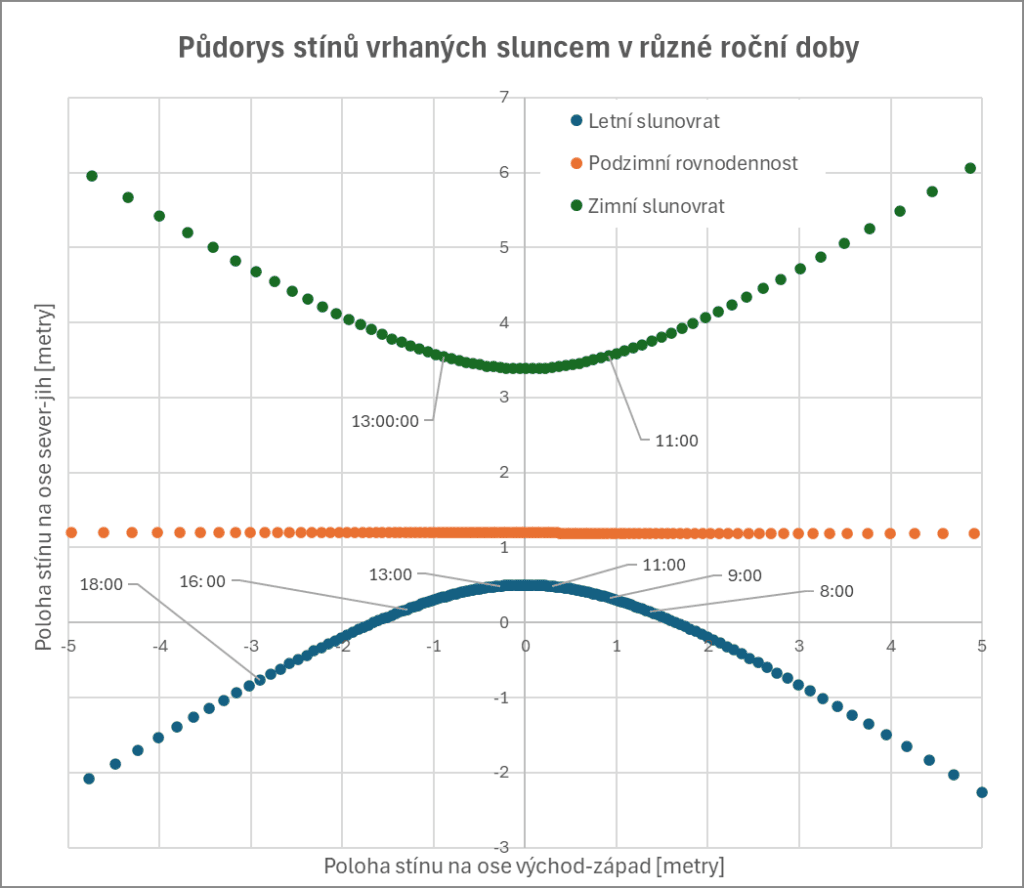
Obrázek 1: Půdorys stínu spočtený pro letní a zimní slunovrat a jarní rovnodennost. Tyčka s délkou jeden metr je umístěna do počátku souřadnicové soustavy. Půdorys je orientován jako standardní mapa, tedy sever je na horní straně grafu. Jednotlivé body stínu jsou od sebe vzdáleny 5 minut. Pro lepší shodu s pravým polednem je použit zimní čas pro všechny tři stíny. Je vidět, že během rovnodennosti je poučka přesná, pro letní a zimní rovnodennost platí pouze během pravého poledne.
Je tedy určité časové okno okolo poledne, kdy tato poučka platí v průběhu celého roku. Ovšem musíme mít na paměti, že jde vždy o pravé poledne. Zrovna pro střední Čechy a zimní čas je odchylka mezi lokálním a slunečním časem velmi malá. Ale mějte na paměti, že v jiné zemi se čas místní a sluneční mohou výrazně lišit. Ovšem i u nás během posunutého letního času je pravé poledne kolem jedné hodiny odpoledne.
Osobně bych se nebál použít tuto poučku kdykoliv během jarního nebo podzimního vandru. V zimě a v létě je to složitější. Můžeme poučku použít během poledne, ale musíme počítat s tím, že se stín kolem poledne pohybuje pomaleji. Lze říci, že chyba této metody vždy bude menší či rovná 40°. Což, pokud nemáte jinou možnost, je lepší než nic. A pokud budete vědět, kde na Zemi přibližně jste a jaké je datum, můžete použít tyto informace k zpřesnění.
Klacík k určování světových stran není žádná novota
Použití klacíku zapíchnutého do země není žádná nová tábornická pomůcka. Ve skutečnosti se jedná o antický nástroj zvaný gnómon, který měl překvapivě mnoho využití a jedním z nich jsou právě i sluneční hodiny.
Pro nejčastější typ slunečních hodin se používá gnómon/tyčka nakloněná. Ale pozor, musí být nakloněná přesně k severu, díky tomu je tyčka rovnoběžná se zemskou osou a trasa stínu se mění během roku jen velmi málo. Značky jednotlivých hodin ale nebudou od sebe vzdálené o stejné úhly. To nastane pouze v případě, že rovina, na kterou značky kreslíte, je kolmá na gnómon, případně pokud stín promítáme na kulovou plochu. V těchto případech lze použít značky hodin stejně daleko od sebe. V obou případech musíte mít gnómon stále nakloněný směrem k Polárce. V ostatních případech bude nutně „ciferník“ slunečních hodin nepravidelný, s nestejnými úhly.
Přesný výpočet pro milovníky matematiky
Na webové stránce sunearthtools.com se dají najít a uložit do tabulky dráhy Slunce kdekoliv na Zemi v kteroukoliv roční dobu. Našel jsem si data pro letní a zimní slunovrat a podzimní rovnodennost pozorovanou z Prahy 6. Potom jednoduchou geometrií dokážeme spočítat polohu stínu na zemi. Pro jednoduchost budeme uvažovat délku tyčky jeden metr a tyčku zapíchnutou kolmo v zemi.
Na začátek je potřeba si definovat důležité pojmy. Trasu neboli trajektorii Slunce na nebi je nejlepší popisovat pomocí úhlů v takzvaných sférických souřadnicích. „Výšku“ Slunce nad obzorem udává sluneční elevace (v rovnicích značka e) neboli úhel mezi lokální rovinou Země a polohou Slunce. Takže během východu a západu slunce bude elevace 0° a během pravého poledne bude tento úhel maximální. Na jaře a na podzim je tento maximální úhel 40°, přes léto vyšplhá Slunce až na 63° a v poledne během zimního slunovratu je pouhých 16° nad obzorem.
Druhým parametrem je poloha Slunce v rámci světových stran. K tomuto se používá úhel zvaný azimut (v tomto případě topografický azimut, značka a), což je úhel měřený od severu po směru hodinových ručiček. Pomocí azimutu a elevace sledujeme polohu Slunce na nebi. Pokud máme oba tyto parametry, můžeme spočítat polohu stínu v libovolný čas a sledovat, jestli dráha stínu skutečně kopíruje směr ze západu na východ.
Pro tento výpočet nám stačí jednoduché goniometrické funkce sinus, kosinus a kotangens.
Délka stínu je dána sluneční elevací a směr, kterým je stín vrhán, je zase daný azimutem. Délka stínu lze vypočítat jako výška použité kolmé tyče (předpokládejme pro jednoduchost jeden metr) vynásobená kotangentem sluneční elevace, neboť stín a klacek tvoří pravoúhlý trojúhelník. Konkrétní vzorce jsou vidět v ilustrativních obrázcích (Obrázek 1 a 2).
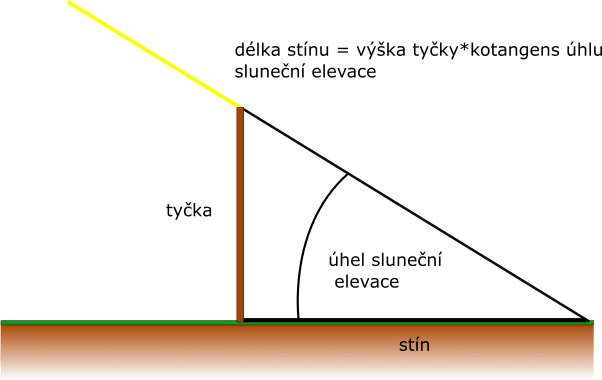
Obrázek 2 (pohled z boku): Délka stínu vrženého kolmo zapíchnutou tyčí na rovném povrchu je dána sluneční elevací a délkou tyče.
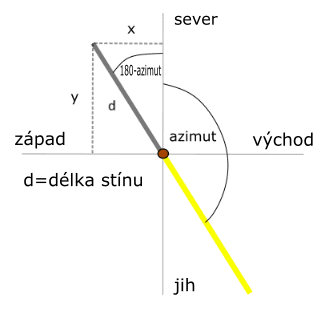
Obrázek 3 (pohled shora): Poloha stínu na rovné zemi je dána úhlem azimutu. Nákres ukazuje pohled shora na tyč kolmo zapíchnutou do země ve středu protínajících se os západ-východ a sever-jih. Žlutě je znázorněn směr, ze kterého svítí slunce. K tomuto směru měříme od severu po směru hodinových ručiček úhel azimutu. Stín pak dopadá v úhlu doplňujícím azimut do 180°.
Pro vyhodnocení otázky je vhodné vytvořit graf, který znázorňuje průběh stínu během dne. K tomu je třeba rozložit polohu stínu do os, z nichž jedna bude odpovídat západovýchodnímu směru a druhá severojižnímu směru. Pokud má uvedená zálesácká poučka fungovat, je důležité, aby se hodnota na severojižní ose měnila co nejméně. Hodnoty průmětů označíme x a y stejně jako na Obrázku 2. Parametr v je výška tyčky a d je délka stínu na zemi. Potom se dají všechny důležité vztahy popsat následujícími rovnicemi:
d=v*cotg(e)
x = d*sin(180-a) = v*cotg(e)*sin(180-a)
y = d*cos(180-a)= v*cotg(e)*cos(180-a)
Pokud dosadíme data ze stránky sunearthtools.com, dokážeme spočítat, jak vypadá půdorys stínů pro vybraná data. Výsledky jsou na Obrázku 3. Pro lepší přehled jsem na určité body v grafu přidal časové značky, ale pozor! Rozhodl jsem se použít data ze sunearthtools.com pouze ve SEČ (středoevropský čas, někdy označovaný nesprávně jako zimní čas), tedy v čase, kdy je pravé poledne podobné poledni v našem časovém pásmu.
Pro Zeptej se vědce odpovídal Jan

