Kolik existuje možných šachových partií?

Děkujeme za krásný dotaz. Někdy se říká, že šachových partií je více než atomů v pozorovatelném vesmíru. Pojďme se na to tedy nejdříve podívat a zároveň nastínit některé trable, které nás při hledání odpovědi na otázku potkají.

Šachy a pozorovatelný vesmír

Nejdříve se musíme zeptat, kolik je atomů v pozorovatelném vesmíru. Toto číslo pravděpodobně poprvé odhadl fyzik a astronom sir Arthur Eddington, proto se mu říká Eddingtonovo číslo, a jeho hodnota se dnes uvádí jako 10⁸⁰ [1]. To je samozřejmě nepředstavitelně velké číslo, pokud 10⁰=1, 10¹=10, 10²=100…, pak 10⁸⁰ je číslo začínající jedničkou a pokračující osmdesáti nulami!

Znamená to, že počet šachových partií je ještě větší než 10⁸⁰? Jak velké je tedy toto číslo? Stejnou otázku si položil v roce 1950 významný americký matematik Claude Shannon a odhadl jej na 10¹²⁰ [2] (a podle něj se mu říká Shannonovo číslo). Chtěl tím poukázat na to, že v té době vznikající počítače nemohli (a stále nemohou) hrát šachy způsobem, kdy se počítá každá varianta, která může nastat – možností je zkrátka příliš mnoho.

Průměrná délka partie je asi 40 tahů

V dnešní době hrají počítače šachy velmi dobře, a to díky rozsáhlým databázím, důmyslným algoritmům pro hledání tahů a zejména ohodnocení pozic, na základě kterého vyberou své tahy. Toto hodnocení tedy umožňuje výběr „nejlepších“ tahů a nemusí tak procházet všech 10¹²⁰ možností.

Nastíníme si, jak k takovému číslu dojít. Správně píšete, že máme omezený počet figurek, na začátku partie konkrétně 32, a pohybujeme jimi na omezeném prostoru – šachovnici s 64 poli. Problém může nastat, pokud budeme uvažovat sekvenci tahů:

1. bílý jezdec na pole f3 – Černý jezdec na pole f6

2. bílý jezdec zpět na původní pole g1 – Černý jezdec na původní pole g8

… a ty stejné tahy se mohou neustále opakovat.

Mohou se tedy jezdci pohybovat od začátku tam a zpět a partie nikdy neskončí? To by mohl být problém, partie by pak trvala tak dlouho, dokud by to šachisty bavilo – teoreticky by tak existovalo nekonečné množství partií.

Shanon raději předpokládal, že průměrná délka partie je asi 40 tahů. Tady je ale důležité upozornit, že když šachisté mluví o 40tahové partii, myslí tím 40 tahů bílého a 40 tahů černého – celkem tedy 80 pohybů figurkami. Shannon si dále všiml, že v průběhu partie má hráč při každém tahu průměrně asi 30 možných příštích tahů. Udělejme krátký výpočet:

1. tah (bílý): průměrně 30 možných partií

v každém tahu z těchto 30 možností má druhý hráč opět průměrně 30 možností, tedy

1. tah (černý): 30×30 = 30² = průměrně 900 možných partií

následuje tah černého a každá z 900 partií má dalších 30 možných pokračování

2. tah (bílý): 30×30×30 = 30³ = průměrně 27 000 možných partií

což pro 40 tahovou partii (která obsahuje celkem 80 pohybů figurkami) je 30⁸⁰ možných partií, a to můžeme upravit na 10¹²⁰.

Průměrný počet možných tahů po každém tahu

Obrovské číslo 10¹²⁰ je tedy pouze odhad založený na dvou předpokladech – 40 tahů na partii a průměrně 30 možných pokračování v určité pozici. Jak je to ve skutečnosti? Například na začátku hry, v tzv. základní pozici, může bílý táhnout pouze pěšci o jedno pole (8 možných tahů), nebo o dvě (8 možných tahů), nebo jezdcem přeskočit řadu pěšců (4 možné tahy), celkem má tedy 20 možných tahů. Černý pak může odpovědět stejným počtem tahů a celkový počet takto vzniklých partií je 20×20=400. Na druhé straně v pozici, kdy se vyskytují na šachovnici pouze věže a dámy, je možných tahů mnoho.

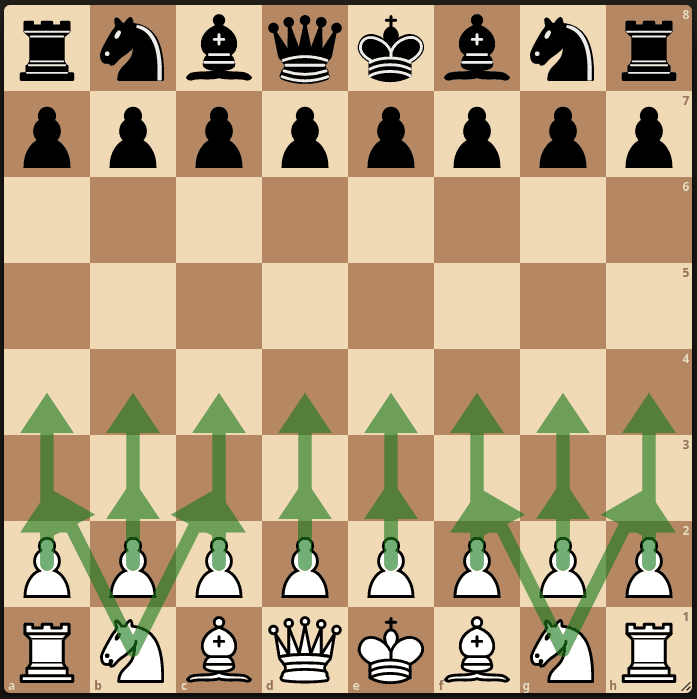
Obrázek: počet možností bílého v základním postavení (20) a v otevřené pozici (54).

Nejdelší možná partie

Nejen počet možností, ale i délka partie se může měnit – od krátkých partií, kde zahrál pouze bílý první tah, až po partie trvající i 200 tahů každého hráče (tedy celkem 400 pohybů figurek). Měnící se délka partií a počet možných tahů značně ztěžují určení přesného množství možných partií. Navíc se nám vrací problém s nekonečným množstvím tahů, tedy taháním figurkami tam a zpět – ten však vyřešili sami šachisté zavedením několika omezujících pravidel: Pokud bude pozice na šachovnici třikrát opakována, nebo v průběhu 50 tahů nedojde k odebrání žádné figury nebo k pohybu pěšce, hráč může reklamovat remízu (tzn. uplatnit nárok na nerozhodný výsledek, automaticky k tomu dochází po pětinásobném opakování a 75 tazích bez braní nebo tahu pěšcem) [3]. Výborně!

Znamená to, že můžeme určit počet tahů nejdelší možné partie? Ano, je to 5900 tahů (tedy 11 800 pohybů figurek) [4]. Skvělé, teď nám už „jen“ zbývá spočítat, kolik je jednotahových partií, dvoutahových… atp. až po nejdelší, 5900tahové partie. Zkusme si to, co jsme si zatím řekli, přehledně sepsat:

Počet pohybů figurek	1	2	3	4	…	11 800
Počet tahů v partii	1	1	2	2	…	5900
Počet možných partií	20	400	8902	197 281	…	??

Poslední řádek nám bohužel naznačuje, že čísla v něm budou rychle růst a přesné číslo získáme jen těžko. Už po 4 pohybech figurkou (tedy 2 tahy bílého a 2 černého) existuje až 197 281 možných partií. Shannonův odhad, 10¹²⁰ partií, byl zpřesněn a nyní se uvádí 10¹²³, vypočítaný pro 40tahovou partii s průměrně 35 možnými tahy na jednu pozici [5].

Odhad počtu „smysluplných“ tahů

Počet všech možných šachových partií zůstává neznámý, každopádně to ale pro nás bude nepředstavitelně obrovské číslo. Zkusme se na problém podívat trochu víc realisticky. Šachy jsou bitva dvou armád a každý hráč se snaží zvítězit zajmutím protivníkova krále – uskutečnění tzv. šachmatu. Mohl by nás tedy zajímat odhad počtu možných „smysluplných“ partií, kdy se oba hráči snaží vyhnout znevýhodňujícím tahům, které by vedly k jejich prohře, například přijít o nejmocnější figurku na šachovnici – dámu. Počet těchto partií odhadneme stejně jako u Shannonova čísla: Budeme předpokládat průměrně 40tahovou partii (tedy opět 40 pohybů figurkou bílého a 40 černého) a v každé pozici průměrně tři rozumné tahy:

1. tah (bílý): průměrně 3 rozumné partie

v každém tahu z těchto 3 možností má druhý hráč opět průměrně 3 možnosti, tedy

1. tah (černý): 3×3 = 3² = průměrně 9 rozumných partií

2. tah (bílý): 3×3×3 = 3³ = průměrně 27 rozumných partií

což pro 40tahovou partii (která obsahuje celkem 80 pohybů figurkami) je 3⁸⁰ možných partií, což můžeme upravit na 10⁴⁰.

Těžko si to představit

Ve srovnání s 10¹²⁰ by se 10⁴⁰ mohlo zdát jako malé číslo – ano, je to menší než počet atomů ve vesmíru (10⁸⁰), ale rozhodně se nejedná o malé číslo.

Můžeme si například vzít sadu 32 mariášových karet a vyskládat je vedle sebe. Na první místo můžeme položit kteroukoliv z 32 karet, na druhou už nám zbyde jen 31, pak 30 atd. Tedy celkový počet možností bude 32×31×30×… = 32! (symbol vykřičníku znamená faktoriál, viz sekci Další čtení), tedy zhruba 10³⁵.

Odhaduje se například, že na Zemi máme 10¹⁷ zrnek písku. Teď si zkuste představit, že každé jedno zrnko písku pošleme na jinou planetu, která také obsahuje 10¹⁷ zrnek. Když dáme všechna zrnka ze všech planet dohromady, pořád to bude milionkrát méně než počet smysluplných partií. Dalším přiblížením tohoto obrovského čísla (10⁴⁰) je třeba počet molekul vody ve Winnipežském jezeru v kanadské Manitobě [6]. Což je na světě 30. největší jezero, které je asi tak velké jako 62 000 rybníků Rožmberk dohromady – opět se jedná o doslova nepředstavitelné množství.

Závěr

Závěrem musíme říct, že matematika bohužel nedokáže na tuto otázku odpovědět a v současnosti se tak můžeme pouze kochat nepředstavitelně velkými odhady.

Pro Zeptej se vědce odpovídal Jakub