Spálí laserová zbraň křečka na vzdálené planetě?

Odpověď v kostce

Dobrý den, váš dotaz je vskutku zajímavý a dobře odráží to, jak si často představujeme lasery. Budeme řešit šíření laseru ve vakuu, kde nedochází k rozptylu světla na částečkách vzduchu nebo prachu. Tím můžeme zanedbat ztráty energie laseru při šíření vesmírem. Ale i když se nebude měnit jeho celková energie, laserový svazek se bude rozbíhat, čímž se bude zvětšovat jeho plocha.

Je třeba brát v úvahu, že 1000 wattů na milimetr čtvereční je poměrně slušný laser, který by vám mohl značně ublížit na zdraví, ale 1000 wattů na metr čtvereční odpovídá slunci za velmi slunného poledne. V praxi se každý laser, který se zatím podařilo vytvořit, alespoň trochu rozbíhá a už při kilometrových vzdálenostech významně klesá jeho intenzita neboli plošná hustota výkonu. Čím větší výkon na čím menší ploše, tím větší bude intenzita laseru. Jak se bude laserový svazek během šíření volným prostorem pomalu rozšiřovat, bude se jeho intenzita postupně zmenšovat.

Toto rozbíhání se v laserovém žargonu nazývá divergence svazku a většinou se určuje v miliradiánech (1 mrad odpovídá 3,437 úhlovým minutám). Šířka laserového svazku se tedy pomalu, ale jistě a rovnoměrně zvětšuje, jak se světlo šíří prostorem.

Pro představu: pokud by laserový svazek s divergencí 1 mrad uletěl 1000 metrů, šířka jeho svazku už by se pohybovala kolem jednoho metru. Toto je důvod, proč se lasery používají v protivzdušné obraně na relativně krátké vzdálenosti. Například systém Iron Beam má mít dosah pouze několik kilometrů, a to i když používá laserový systém s ohromným výkonem 100 kW. Můžeme tedy říct, že se o křečka žijícího mimo Sluneční soustavu není třeba vůbec bát.

Trochu více té fyziky

Divergence laserového svazku nutně vyplývá z jeho prostorové geometrie. O prostorové geometrii laserového svazku lze obecně říct pouze to, že je to nějaké řešení Helmholtzovy paraxiální rovnice [1]. Paraxiální znamená, že se světlo šíří převážně v jednom směru, což se děje právě u laserů.

Řešit tuto rovnici je poměrně složité, ale nebojte, v tomto textu se jí vyhneme. Z praxe totiž víme, že nejčastějším tvarem, nebo, chcete-li, nejčastějším řešením této rovnice je takzvaný gaussovský svazek [2]. Gaussovský svazek má tu výhodu, že kromě toho, že je to opravdu nejčastější typ laserového svazku, tak i má velmi jednoduchý vztah pro hodnotu divergence. Ten se dá nalézt třeba zde [3] a vypadá následovně:

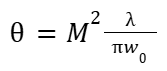
kde θ je divergenční úhel (nebo též půlúhel), M² je parametr kvality, který je v dokonalém gaussovském svazku roven jedné, jinak vždy větší než jedna, je vlnová délka použitého světla a w₀ je šířka svazku v nejužším místě. Tedy můžeme říct, že jsme schopni zmenšit divergenční úhel zmenšením vlnové délky a zvětšením šířky laserového svazku, ale nic z toho nejde v praxi do nekonečna, takže laser vždy nějakou divergenci bude mít. Navíc, pokud nebude svazek dokonale gaussovský, vyjde divergence ještě větší.

Příklad s oblíbeným laserem

Pro ilustraci: Vezměme velmi oblíbený laser tvořený heliem a neonem, takzvaný HeNe laser. Ten má nejčastěji vlnovou délku 632,8 nm. Pokud budeme uvažovat M² rovno 1 a šířka svazku v nejužším místě 1 milimetr, vyjde nám ze vzorce divergenční úhel 201 μrad. Toto odpovídá asi jedenácti miliontinám úhlového stupně. Na krátkých vzdálenostech nepozorovatelné, ale po deseti kilometrech se z milimetrového svazku stane čtyřmetrový. A protože hustota energie klesá s kvadrátem plochy, bude po deseti kilometrech svazek 16 000 000 krát méně intenzivní.

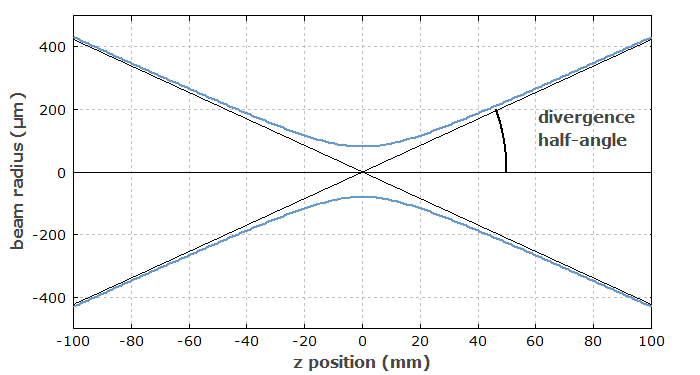
Obrázek 1: Graf znázorňující, jakou roli hraje θ v divergenci svazku. Z obrázku je patrné, proč se θ značí jako půl úhel, v angličtině tedy: divergence half-angle. Na svislé ose je šířka svazku a na vodorovné je vzdálenost ve směru šíření svazku.

Ale čistě hypoteticky to nelze vyloučit

Nechme teď stranou prvotní představu laseru pálícího po dronu gaussovským svazkem a položme si otázku: Je nějaké řešení oné Helmholtzovy paraxiální rovnice, které má nulovou divergenci? Odpověď je ano. Bohužel, to, že řešení rovnice existuje, ještě neznamená, že se nám podaří pro toto řešení sestrojit skutečný laser.

Jedním z oněch řešení je takzvaný besselovský svazek, který sice nediverguje, ale zase k jeho vytvoření potřebujete nekonečně mnoho energie, takže se nepovažuje za reálný. Existuje ovšem jistý kompromis, a to svazky bessel-gaussovské, přičemž ve zdroji [4] popisují vědci vygenerování těchto laserových svazků s divergencí v mikroradiánech.

A jak to tedy dopadne s oním mimozemským křečkem?

Jestli se někdy podaří vytvořit v laboratoři zcela nedivergující svazek, nevím. Někteří tvrdí, že jsou jisté fyzikální bariéry, které tomu brání. Podaří se někdy vytvořit laserový svazek, který dokáže cestovat 200 světelných let a spálit mimozemského křečka? Spíše ne. Ale s konečnou platností to zatím vyloučit nemůžeme.

Pro Zeptej se vědce odpovídal Jan