Jelikož jde o jeden z nejtechničtějších dotazů v tomto oboru, který jsme kdy dostali, pokusím se nejdřív o stručný úvod, který snad zároveň i dalším případným čtenářům pomůže pochopit, na co se tazatel ptá a na co my odpovídáme. 

Tzv. standardní model částicové fyziky je základní teorií popisující vlastnosti a chování všech elementárních částic, které tvoří svět kolem nás – tedy takových částic, o kterých dnes nevíme, že by se skládaly z nějakých dalších částic. Popisuje tedy věci jako fotony, elektrony a kvarky, ale už ne přímo třeba proton, protože ten se skládá z kvarků. 

Vzájemné působení těchto částic je ve standardním modelu popsáno třemi základními interakcemi – silami: elektromagnetickou, slabou a silnou. Vliv čtvrté základní interakce, gravitace, je za hranicemi tohoto modelu. Tyto síly lze v rámci standardního modelu (alespoň v některých situacích) chápat jako tzv. výměnné interakce: dvě částice, které na sebe působí, si mezi sebou vyměňují jinou (nebo někdy i stejnou) částici, která je „nositelem“ dané síly. (Vzhledem k rozmanitosti druhů interakcí částic mezi sebou však tento popis není vždy zcela přesný.)

Elementární částice mají tu zajímavou vlastnost, že nemají žádný rozměr ani tvar – mají hmotnost, náboj a několik dalších „částicových“ vlastností, ale nelze si je v žádném případě představovat jako „malé kuličky“. I přesto však mohou mít moment hybnosti – tedy se jevit jako rotující (otáčející se v prostoru; i když nemají žádný opravdový tvar!). Tomuto momentu hybnosti říkáme spin a každý druh částice má spin předem dané velikosti, která ve vhodných jednotkách v principu nabývá pouze hodnot 0, ½, 1 atd. 

Částice, jejichž spin je celé číslo, se nazývají bosony. Bosonů se může v libovolném místě prostoru vyskytovat libovolné množství (pokud nejsou třeba elektricky nabité, tím se odpuzují). Částice s poločíselným spinem se nazývají fermiony. Pro ty platí, že „ve stejném kvantovém stavu“ se nemůže vyskytovat víc než jeden fermion. Vysvětlit zcela přesně, co to znamená, by bylo složité – ale zjednodušeně můžeme říci, že pokud mají fermiony sdílet nějakou příliš malou oblast v prostoru, musí se lišit ještě dalšími vlastnostmi než polohou – např. velikostí a směrem hybnosti nebo orientací spinu. Přesně tato vlastnost je klíčová pro funkci fermionů jako základních kamenů hmoty. Právě proto, že elektrony jsou také fermiony, mají elektronové obaly atomů složitou strukturu, která umožňuje popsat jejich odlišné energetické stavy a která je zodpovědná za celou chemii – kdyby byly elektrony bosony, tak jsou všechny elektrony v atomech ve stejném stavu, a sice v tom nejnižším. Naopak bosony obvykle hmotu netvoří a potkáváme se s nimi především jako se zprostředkovateli interakcí. Zdaleka nejznámějším bosonem je foton – základní částice světla a zprostředkovatel interakce elektromagnetické.

Standardní model popisuje svět jazykem kvantové teorie pole. V tradičním přístupu kvantová teorie pole vzniká formálně tzv. kvantováním klasické teorie pole. To zní poměrně abstraktně, ale pro nejjednodušší případ nemusíme chodit daleko – kvantová elektrodynamika, popisující interakce nabitých částic a fotonů, je zkrátka kvantovou verzí elektrodynamiky klasické, popsané Maxwellovými rovnicemi. Velmi zajímavou vlastností procesu kvantování je, že každému poli je přiřazena částice a spin této částice je přímo dán vlastnostmi tohoto pole. Poli skalárnímu (tedy takovému, které každému bodu v prostoru přiřazuje jedno číslo, které nezávisí na soustavě souřadnic) přísluší částice o spinu 0, zatímco poli vektorovému (které každému bodu přiřazuje vektor, tedy kombinaci velikosti a směru, na jehož otočení vůči soustavě souřadnic záleží) přísluší částice o spinu 1. 

Pokud jste zvědaví na nějaký příklad, tak vězte, že foton má spin 1 a vznikne kvantováním elektromagnetického pole. To se v klasickém popisu skládá ze dvou vektorů – intenzity elektrického pole E a magnetické indukce B. K jeho úspěšnému kvantování však musíme pracovat v jazyce speciální teorie relativity, která operuje s vektory v prostoročase, tzv. čtyřvektory. Takový objekt, který – jak už jeho název napovídá – má čtyři složky, je z vektorů E a B (každý o třech složkách) obtížné přímo vytvořit. Naopak velmi snadné je to udělat kombinací skalárního potenciálu φ (o jedné složce) a vektorového potenciálu A (o třech složkách) – dvou veličin, z nichž lze i ve formalismu Maxwellových rovnic snadno určit E a B.

To, že je foton vektorová částice (tedy o spinu 1), vůbec není náhoda. Pokud si vezmeme ony tři známé síly uvedené v dotazu – elektromagnetickou, slabou a silnou – tak skutečně mechanismus, jakým je ve standardním modelu implementujeme, přirozeně vede k vektorovým bosonům pro všechny tři tyto interakce. Abychom alespoň částečně vysvětlili, proč to tak je, musíme trochu zabřednout do detailů Lagrangeovy teorie pole. 

Jejím základním prvkem nejsou rovnice popisující pole (jako třeba Maxwellovy rovnice v elektromagnetismu), ale tzv. lagrangián – funkce, která je definovaná v každém bodě prostoru. Její hodnota v tomto bodě je vždy funkcí hodnot všech relevantních polí v tomto bodě, případně jejich derivací. Ze znalosti lagrangiánu v klasické teorii pole můžeme odvodit rovnice, podle kterých se chování polí řídí; z jeho znalosti v kvantové teorii pole můžeme odvodit, jaké částice v naší teorii jsou, jaké mají hmotnosti, náboje a další vlastnosti a jak spolu navzájem interagují.

Lagrangián je skalární veličina – to znamená, že jako funkce každému bodu v prostoru přiřazuje jednu hodnotu, která se nezmění, pokud vhodným způsobem přejdeme k jiné soustavě souřadnic v tom prostoru – a to i přesto, že hodnoty polí v lagrangiánu obsažených se takovou transformací mění (pokud tato pole nejsou skalární). Takovéto neměnnosti vůči nějaké transformaci říkáme symetrie. Skalárnost lagrangiánu konkrétně zajišťuje jeho symetrii vůči všem transformacím souřadnic povoleným v rámci speciální teorii relativity, tedy přechodu do souřadnicových systémů, které jsou vůči původnímu otočené nebo se vůči němu rovnoměrně přímočaře pohybují. Jeden z klíčových stavebních kamenů moderní teoretické fyziky – teorém Noetherové – říká, že každá symetrie znamená existenci zákona zachování nějaké veličiny – symetrie vůči otočení souřadnic má například za následek zachování momentu hybnosti. 

Kromě symetrie hrají ve fyzice vůči transformaci souřadnic významnou roli také symetrie vůči transformacím polí samotných. Zatímco symetrie fyzikálních zákonů vůči otáčení je věc, kterou si asi dovedeme představit, tady se jedná o záležitost bez jednoduché fyzické paralely – a tak si k jejímu vysvětlení budeme muset vzít na pomoc několik jednoduchých rovnic. Lagrangián jednoho skalárního pole φ, které v každém bodě prostoru a času nabývá nějaké komplexní hodnoty a které s ničím neinteraguje (ani samo se sebou), můžeme napsat například jako:

,

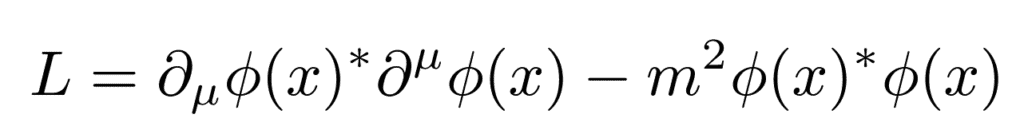
kde * označuje komplexní sdružení, derivace s indexem značí derivaci podle jedné ze čtyř prostoročasových souřadnic (tří prostorových a jedné časové) a přes možné hodnoty indexu μ se sčítá. Veličina m je hmotnost částice, která poli přísluší. Derivace v prvním členu jsou nezbytným prvkem lagrangeovské teorie – objekt, v jehož lagrangiánu by derivace nebyly, není schopen žádného vývoje nebo pohybu.

Že je tento lagrangián skalárem (tedy že je neměnný vůči transformacím speciální teorie relativity), nahlédneme snadno za pomocí čtyřvektorového formalismu speciální teorie relativity: každý výraz, který je tvořen skaláry, vektory a derivacemi, je skalární právě tehdy, když z něj „nevisí žádný index“ – ke každému indexu „dole“ najdeme stejný index „nahoře“ a každá takováto dvojice indexů znamená sčítání přes všechny čtyři složky čtyřvektorů.  Kromě toho si ale povšimněte, že náš lagrangián se také nezmění, pokud celé pole φ vynásobíme komplexním číslem, jehož absolutní hodnota je 1, tedy číslem ve formátu c = exp(i × θ). Komplexní sdružení pole se totiž při takové transformaci vynásobí faktorem c*=exp(-i × θ), a protože se v obou členech vyskytuje součin pole a jeho sdružení, výsledná hodnota se prostě násobí jedničkou.

Aby tato symetrie ovšem fungovala tak, jak je, musí být „globální“ – musíme pole vynásobit v každém bodě prostoročasu stejným číslem. Proč? Protože v prvním členu jsou derivace! Pokud by náš faktor c byl funkcí polohy, tak derivace v prvním členu působí i na něj – transformovaný lagranigán pak má následující formu: 

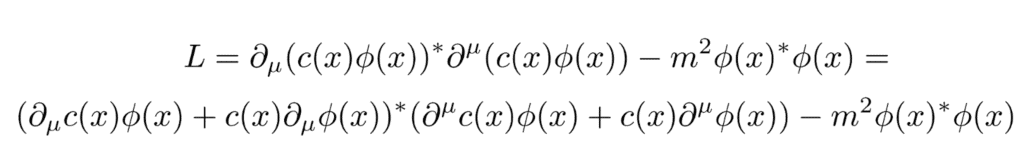
Roznásobením dvou závorek vzniknou čtyři členy, v posledním z nich se c(x) a c*(x) „požerou“ tak, jak bychom chtěli, ale zbylé tři členy s derivacemi c(x) jsou zřejmě odlišné od původního lagrangiánu! Pokud bychom chtěli, aby náš lagrangián byl neměnný vůči lokální transformaci pole, tak naše jediná možnost je zavést další, pomocné pole, které se bude při naší transformaci měnit právě tak, aby se langrangián jako celek zachoval. To bude fungovat například, pokud budeme uvažovat lagrangián: 

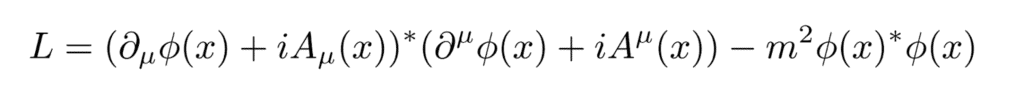
Na první pohled není jasné, jak moc jsme si teď pomohli, dokud si neuvědomíme, že předpis toho, jak bude transformace vypadat pro různá pole, je pořád zcela na nás! A tak můžeme uvažovat transformaci, při níž platí: 

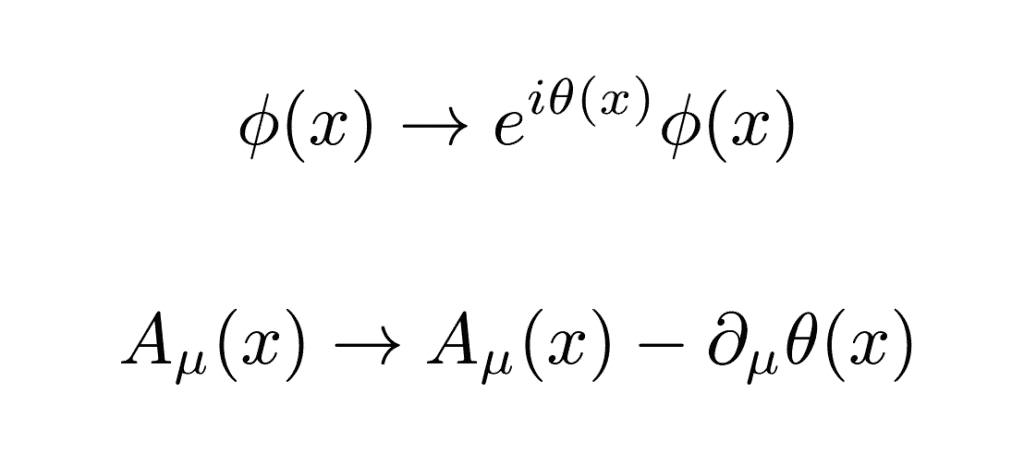
Že je náš nový Lagrangián vůči takové transformaci neměnný, to už necháme čtenáři jako cvičení, ať se naše odpověď nenafoukne v učebnici kvantové teorie pole. Daň, kterou jsme za tuto neměnnost zaplatili, je, že jsme museli zavést nové pole – všimněte si, že toto pole je, na rozdíl od našeho původního skalárního pole, (čtyř-)vektorové. K tomu nás „donutila“ nezbytná přítomnost derivací a speciální teorie relativity, která vždy vyžaduje, aby se derivovalo postupně podle všech složek čtyřvektoru. 

V tuhle chvíli podle návodného označení už laskavý čtenář asi tuší, že pole A odpovídá vektorovému potenciálu v elektromagnetismu, a tedy fotonu a že jsme si tady tak vlastně mimochodem odvodili lagrangián pro kvantovou elektrodynamiku (ač tedy pouze pro skalární pole). Podobné cvičení je možné udělat i pro slabé a silné interakce a získáme z něj W+Z bosony pro slabé interakce a gluony pro silné interakce – formální provedení je ovšem mnohem složitější, protože symetrie, jejichž zachování bychom vyžadovali, lze vyjádřit jen pomocí matic a jejich násobení, do čehož se již pouštět nebudeme. Vždy však zůstane v platnosti pozorování, že přítomnost derivací nás nutí do formulace nového pole jakožto čtyřvektoru.

Z tohoto popisu je hned jasné, že skalární Higgs (jehož pole tedy v každém bodě prostoročasu nabývá jenom jedné hodnoty, nikoliv celého vektoru), nereprezentuje žádnou takovou „lokální“ (v každém bodě jinou) symetrii lagrangiánu – naopak, Higgs souvisí se symetrií globální, která je však „spontánně narušená“ – což vede k Higgsovu mechanismu tvorby hmoty. 

Tyto úvahy jsou však do určité míry formální a obecné – vedou k dobrému konceptuálnímu popisu toho, co je „síla“ a co je „nositel“ síly; na druhou stranu je ale kvantová realita vždycky o něco složitější. Dobře si to můžeme popsat na případu staré známé elektromagnetické interakce. Interakci mezi dvěma elektrony lze skutečně velmi dobře popisovat jako výměnu virtuálního fotonu mezi nimi, a to za pomoci příslušného  Feynmanova diagramu (obr. 1). 

Feynmanovy diagramy na první pohled vypadají jako dětské malůvky, ale mají svá jasná pravidla a ve skutečnosti reprezentují složité matematické výrazy, které z nich lze podle těchto pravidel jednoznačně vytvořit. Klíčová pravidla pro jejich konstrukci jsou, že z obrázku musí „trčet“ přesně ty částice, jejichž interakce právě uvažujeme, že žádná čára nesmí jen tak někde začínat nebo končit v prostoru a že pro každou fyzikální teorii je povolena jenom určitá, přesně specifikovaná množina „vrcholů“, kde se různé čáry potkávají. V kvantové elektrodynamice je dokonce povolen jen jediný vrchol, ze kterého jdou dvě čáry elektronů a jedna fotonu – a všechny jevy, které chceme popsat, musí být kombinací takových vrcholů. Na obr. 1, jakožto ve všech diagramech v odpovědi, probíhají jevy v čase „odshora dolů“. Rovné čáry jsou elektrony a vlnité fotony – tzn. na obr. 1 vidíme dva elektrony, které se k sobě přiblížily, vyměnily si foton, tím změnily směr a zase se „vydaly pryč po svých“, zcela v duchu zjednodušeného konceptu, že elektromagnetismus je výměnná interakce mezi nabitými částicemi zprostředkovávaná výměnou fotonů. 

Ale už třeba při Comptonově rozptylu fotonu na elektronu (obr. 2) nebo anihilaci elektronu s pozitronem (obr. 3) tento popis trochu vázne, jelikož částice „uvnitř“ diagramu je pořád elektron. Ještě pořád ho můžeme vidět jako „pokračování“ toho elektronu, který do interakce vstoupil, ale tato touha nás jistě brzy opustí, když se podíváme na diagram rozptylu fotonu na fotonu (obr. 4), kde je celá interakce zprostředkovaná zcela virtuálním elektronem! (Rozptyl fotonu na fotonu je „čistě kvantový jev“ – to se pozná podle toho, že neexistuje graf, který by následoval výše zmíněná pravidla o čarách a vrcholech a přitom jej popisoval bez uzavřené smyčky z částic. To znamená, že pokud bychom příslušnou teorii pole řešili klasicky – což v podstatě znamená řešit Maxwellovy rovnice – o existenci jevu se nedozvíme. Útěchou nám může být, že neuděláme moc velkou chybu v předpovědi, protože jde o jev velmi obtížně pozorovatelný.)

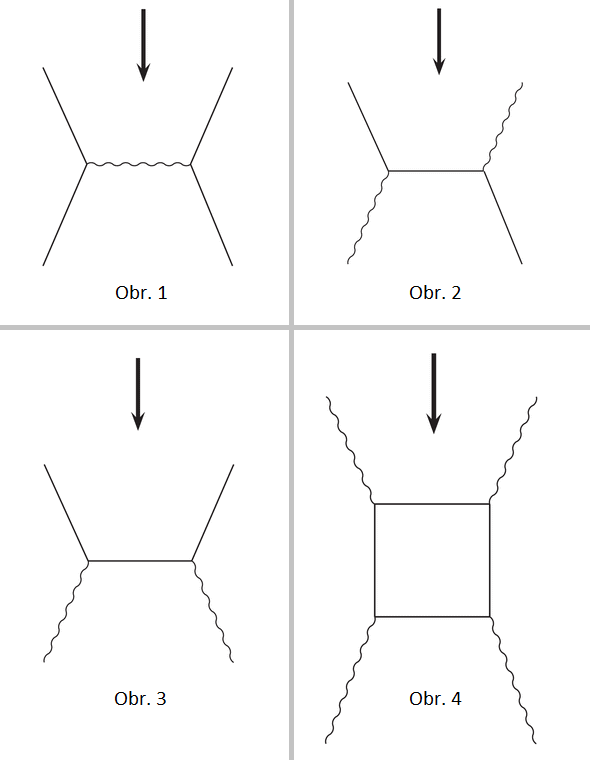
Obr. 1 – Rozptyl dvou elektronů.

Obr. 2 – Rozptyl fotonu na elektronu.

Obr. 3 – Anihilace elektronu a pozitronu.

Obr. 4 – Ano, i rozptyl fotonu na fotonu existuje!

Kvantová teorie, jakkoliv je složitá, se skutečně dá do určité míry zjednodušit na kreslení Feynmanových diagramů. V takovém případě lagrangián slouží jako návod – říká nám, jaké existují částice, tedy „které čáry můžeme kreslit“, a jaké jsou mezi nimi interakce, tedy „které vrcholy jsou povolené“ – a procesy, které teorie předpovídá, jsou ty, pro něž vymyslíme nějaký vhodný diagram. (Hodí se dodat, že ke každému diagramu umíme potom pomocí lagrangiánu přiřadit číslo – pravděpodobnost, že takový proces nastane. Ta nicméně za určitých podmínek může vyjít nulová, takže mohou existovat procesy, které mají příslušný diagram, ale nikdy nenastanou.)

Jak už jsme uvedli, kvantová elektrodynamika má pravidla velmi jednoduchá – jediný povolený typ vrcholu je vždy tvořený nějakou (jakoukoliv) nabitou částicí, která do vrcholu přichází i z něj odchází, a jedním fotonem (jediná další komplikace nastává v tom, že čára, která není foton, může reprezentovat částici i její antičástici, s čímž si ale není třeba dělat starosti v rámci tohoto vysvětlení). Slabá interakce je už o dost složitější, protože povoluje vrcholy, kde se s W bosonem potkávají dvě různé částice (a tím umožňuje změnu identity částic, a tím jejich rozpad). 

Dále je také v lagrangiánu standardního modelu pro každou hmotnou částici k dispozici vrchol „částice-částice-Higgs“, tzn. v principu si lze představit diagramy, kde si dvě hmotné částice „vymění virtuální Higgsův boson“ místo například fotonu. Jim odpovídající numerické hodnoty jsou ale za podmínek relevantních v dnešním vesmíru tak malé, že tato „síla“ má jenom velice malý vliv na jakékoliv reálné jevy. Jelikož vazbová konstanta přiřazená „Higgsovým vrcholům“ je – vzhledem k charakteru Higgse nepříliš překvapivě – úměrná hmotnosti účastnící se částice, jde o korekci důležitou především pro ty nejhmotnější částice. Nepřekvapí, že poprvé byla měřena pomocí té úplně nejtěžší známé částice, top kvarku [1]. 

Z tohoto pohledu tedy vlastně můžeme považovat Higgsův boson za nositele nějaké interakce (nejlépe asi slabé jaderné interakce, neboť vrcholy, které jeho výměnu umožňují, se v lagrangiánu objevují právě kvůli spontánnímu narušení její symetrie), ale když se podíváme třeba právě na obr. 4, tak zjišťujeme, že úplně stejně si roli „nositele“ elektromagnetické interakce občas, tak trochu z nutnosti, může zahrát kromě fotonu i elektron – a popravdě každá částice s nenulovým nábojem. V kvantovém světě zkrátka nikdy nic není tak jednoduché, jak se na první pohled zdá, a mnohé koncepty zavedené „pro přehlednost“ mají jen omezenou praktickou aplikaci.

Pro Zeptej se vědce odpovídal Honza

Zdroje:

[1] CMS collaboration, PRD 100 (2019) 072007. https://journals.aps.org/prd/abstract/10.1103/PhysRevD.100.072007