Předně, výpočty, které zde uvádíme, jsou záměrně zjednodušené, ale o to více názorné. Nejprve si upřesněme zadání. Předpokládejme, že padá lezec těžký 130 kg, a to tak, že od poslední karabiny ho dělí 1 m lana. To znamená, že jeho pád bude dlouhý 2 m. Poslední karabina se nacházela ve výšce 3 m od jističe, tj. celková délka použitého lana byla 4 m (viz obrázek 1). Dále předpokládejme, že lano má statické prodloužení 7,6 % [1].

Nejprve spočítejme sílu pádu za předpokladu, že při pádu lezce se jistič nepohne. Pro výpočet budeme potřebovat teoretický pádový faktor [2] a dynamický elastický modul lana. Teoretický pádový faktor je podílem délky pádu a délky lana, v našem případě 0,5. Teoretický pádový faktor se liší od pádového faktoru [3] používaného v praxi, kde se počítá jen s délkou lana k první karabině, v našem případě by měl hodnotu 2. Dynamický elastický modul lana vypočteme ze znalosti statického prodloužení lana jako 10,3 kN. Pro samotný výpočet síly vyjdeme ze zákona zachování energie. V každém okamžiku pádu platí, že padající lezec přeměňuje potenciální energii v gravitačním poli na kinetickou energii svého pádu a elastickou energii protahujícího se lana [4]. Po několika úpravách dostaneme kvadratickou rovnici pro sílu pádu, která závisí na hmotnosti lezce, pádovém faktoru a elasticitě lana. Dosazením dostaneme hodnotu 5,1 kN.

Bylo-li by jištění založeno jen na principu jednoduché kladky, na jističe o hmotnosti 50 kg by působila gravitační síla o velikosti 0,5 kN směrem dolů a síla pádu o velikosti 5,1 kN směrem vzhůru. V takové situaci bude nebohý jistič pádem lezce katapultován vzhůru se zrychlením o velikosti 92 m/s²! Pro představu, na horské dráze působí maximálně zrychlení o velikosti 50 m/s² [5].

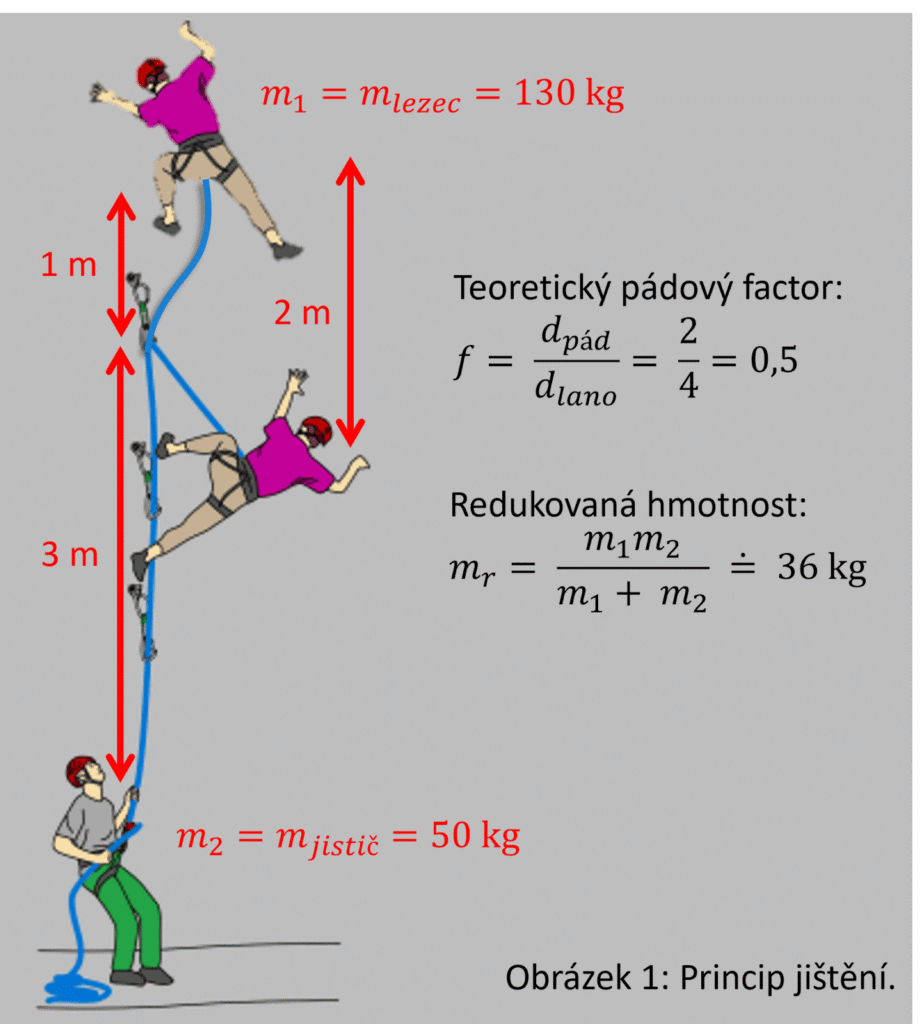
Problém tohoto výpočtu je, že zanedbává pohyb a hmotnost jističe při pádu lezce. Tento nedostatek odstraníme tak, že nebudeme při výpočtu uvažovat jen gravitační působení na lezce, ale i na jističe, a dále hmotnost lezce nahradíme redukovanou hmotností [6] lezce a jističe, která je přibližně 36 kg. Po dosazení dostaneme sílu pádu o velikosti 2,7 kN. Při této síle bude jistič katapultován se zrychlením o velikosti 44 m/s², tedy přibližně o polovinu menším.

Výpočet síly pádu je zásadní pro rizika spojená s pádem jak z pohledu lezce, tak jističe. Příliš velká síla pádu, kterou musí tělo lezce absorbovat, může vést k závažným zdravotním následkům. Ale ani pro jističe není bez rizika, jelikož může být touto silou katapultován do vzduchu a narazit na stěnu. Naštěstí jištění na laně pomáhá třecí síla, která působí proti směru síly pádu, a tzv. dynamické jištění, které vede k minimalizaci pádového faktoru, a tedy síly pádu. Při správném jištění dojde k rozložení síly pádu mezi lezce, jističe a tření mezi lanem a jisticími prvky. Ale i tak je velký rozdíl v hmotnosti mezi jističem a lezcem rizikový. Například Německý alpský spolek [7] doporučuje maximální hmotnostní rozdíl mezi lezcem a jističem 10 kg. Pakliže je rozdíl větší, je nutné použít speciální jisticí pomůcky, které zvyšují tření, a tak usnadní jističi jeho práci [8]. Tak hlavně opatrně!

Pro Zeptej se vědce odpovídal Vítek