Děkujeme za zajímavý dotaz. Rádi bychom zdůraznili, že rozhodně není na místě se cítit trapně, žádná otázka není hloupá! Dezinformací ohledně ne-kulatosti Země je celá řada, a tak se dalo čekat, že podobný dotaz doputuje i k nám. Dokonce se nám v krátkém čase sešly dotazy hned dva. Proto vás odkážeme i na dotaz č. 839 [1], kde rozebíráme jednoduché experimenty, které kulatost Země názorně dokazují.
Hned zkraje uveďme, že Země je kulatá. Tento fakt plyne z mnoha pozorování, které lidstvo provádělo od nepaměti, konkrétně od starověku. My ale začneme příkladem, který je velmi intuitivní a jehož platnost si můžeme ověřit na konci každého roku, kdy ohňostroji vítáme rok nový.
Představme si na chvíli, že Země není kulatá, ale placatá. Jelikož naše každodenní zkušenost říká, že dochází ke střídání dne a noci, znamená to, že i plochá Země by se otáčela kolem své osy. Problém je, že na ploché Zemi by Slunce vycházelo všude na planetě přibližně ve stejný čas. To si můžeme vyzkoušet se stolní lampičkou a knihou, kterou budeme otáčet například okolo osy procházející jejím hřbetem. Když bude vzdálenost mezi knihou a lampičkou dostatečně velká, zjistíme, že přebal knihy bude při jejím otáčení osvícen ve stejný okamžik. Jinými slovy příchod nového roku by se ohňostroji oslavoval ve stejný čas bez ohledu na to, budeme-li slavit v Sydney, Praze nebo Los Angeles. Ale jak ze zpráv v televizi víme, nový rok nastane nejdříve v Sydney, pak v Praze a nakonec v Los Angeles. To je možné jen na kulaté Zemi, kde Slunce osvětluje povrch postupně s jeho otáčením. Proto Slunce vychází nejdříve nad Japonskem, pak zbytkem Asie, Evropou a nakonec Amerikou.
V důsledku kulatosti Země se také liší délka osvitu povrchu v závislosti na poloze, např. za polárním kruhem dokonce nastávají až půl roku trvající polární dny a noci. To, že Slunce vychází na různých místech v různou dobu, bylo v minulosti matoucí a znesnadňovalo celosvětovou komunikaci. Proto byla zavedena časová pásma, která sjednocují oblasti přibližně 15° západně a východně od daného poledníku, přičemž základní časové pásmo, tzv. nultý poledník, prochází Královskou observatoří v Greenwichi v Londýně. Tyto oblasti pak používají stejný čas. Na ploché Zemi by nebylo toto členění nutné, protože pro celou Zemi by stačilo jediné časové pásmo [2, 3].
Historicky první, kdo tvrdil, že Země je kulatá, byl řecký filozof Pythagoras a jeho žák Platon již v 6. století př. n. l. Avšak teprve Aristotelés tuto hypotézu podpořil důkazy ve 4. století př. n. l. Například pozoroval vzdalující se lodě postupně mizící za obzorem nebo tvar zemského stínu na povrchu Měsíce během jeho zatmění. Kolem roku 250 př. n. l. matematik Eratosthenés poprvé změřil obvod Země. Experiment spočíval v porovnání délek stínů (přesněji úhlů dopadu slunečních paprsků) na různých místech zemského povrchu, které leží na stejném poledníku. Konkrétně se jednalo o města Asuán (což je dnešní označení pro tehdejší Syéné) a severněji ležící Alexandrii. Měření probíhalo ve stejném čase, v době letního slunovratu, kdy v Asuánu dopadají sluneční paprsky kolmo k zemskému povrchu (tedy pod úhlem 0°), kdežto v Alexandrii pod úhlem 7,2°. To, že tyto úhly nejsou stejné, je přímým důkazem kulatosti naší planety. Z rozdílu těchto úhlů následně Eratosthenés vypočítal obvod Země mezi 39 060 km a 40 320 km, což je obdivuhodně přesný výsledek vzhledem k podmínkám jeho experimentů [2].
Existují ale i další důkazy kulatosti Země. Tím nejjednodušším je vyletět na oběžnou dráhu Země a na naši modrou planetu se podívat. Zjistíme, že je opravdu kulatá, stejně jako další tělesa ve Sluneční soustavě. Vzhledem k tomu, že všechna tělesa Sluneční soustavy vznikla v důsledku gravitačního působení, je nepravděpodobné, že Země by byla jako jediná planeta ve Sluneční soustavě placatá [4–6].
Měsíc a jeho pozorování je dalším dobrým příkladem. Kdyby byla Země plochá, byl by Měsíc viditelný současně na všech místech na Zemi ve stejný okamžik, ale v důsledku jeho oběhu okolo ploché Země by se měnila jeho zdánlivá velikost a orientace podle toho, kde na Zemi by se nacházel pozorovatel. Pozorování Měsíce toto chování nepotvrzují, a tak máme další důkaz o kulatosti Země [5].
V neposlední řadě je důkazem kulatosti Země gravitace, respektive směr gravitačního působení do středu Země bez ohledu na polohu na zemském povrchu. Pokud by byla Země placatá, gravitace by opět působila do jejího středu. To by ale vedlo k tomu, že její směr by závisel na poloze na ploché Zemi, a proto by na většině zemského povrchu působila gravitace šikmo. V důsledku toho by stromy nerostly kolmo dolů k povrchu, ale byly by mírně nakloněné (zde není myšlen nahodilý šikmý růst stromů, který v přírodě samozřejmě pozorujeme, ale v případě, který diskutujeme, by stromy rostly šikmo na velkém území). Takovéto jevy však nebyly nikde na povrchu Země pozorovány, a tak můžeme opět shrnout, že Země je kulatá [7, 8, další informace viz odkaz v sekci Další čtení].
Na YouTube se nedávno objevilo video, které má dokazovat, že Země není kulatá. Pomocí teleobjektivu je prý podle videa možné z Izraele vyfotografovat Krétu, která je vzdálena 991 km. Avšak jednoduchými trigonometrickými výpočty ukážeme, že to není možné, jak už v Antice věděl Aristotelés. Problém spočívá v zakřivení Země, které se projevuje jako obzor, za který není z daného místa vidět, pakliže pozorovaný objekt za obzorem není velmi vysoký. Aby bylo přes obzor vidět z Haify v Izraeli na Krétu, musela by nejvyšší hora Kréty dosahovat výšky přibližně 64 km, tedy přibližně sedminásobek výšky Mt. Everestu. Ale jelikož je Mt. Everest nejvyšší hora na Zemi, dojdeme k tomu, že žádný vrchol na Krétě nemůžeme z Izraele pozorovat, jelikož nám v cestě stojí obzor. Další důkaz kulatosti Země: byla-li by Země plochá, byl by Mt. Everest byl vidět odevšad, jenže není. Domnělé vrcholy hor na videu tak byly patrně ve skutečnosti mraky promítající se před zapadající Slunce.
Pro fajnšmekry ukážeme i výše zmíněný výpočet, tedy jestli je možné z Haify v Izraeli vidět až na Krétu.
Začneme tím, že si celou situaci převedeme na trigonometrický problém. Vzdálenost horizontu závisí na výšce oka pozorovatele od povrchu Země (h): čím výše budeme, tím dále od nás bude horizont (d). Když si tyto údaje zaneseme do jednoduchého diagramu, tak jako na obr. 1, vidíme, že celý výpočet se zjednoduší na řešení Pythagorovy věty. Horizont je vyznačen bodem H, z kterého vedeme tečnu k oku pozorovatele ve výšce h nad povrchem Země, která má známý poloměr r. Vznikl nám pravoúhlý trojúhelník s přeponou délky r + h a odvěsnami r a d.
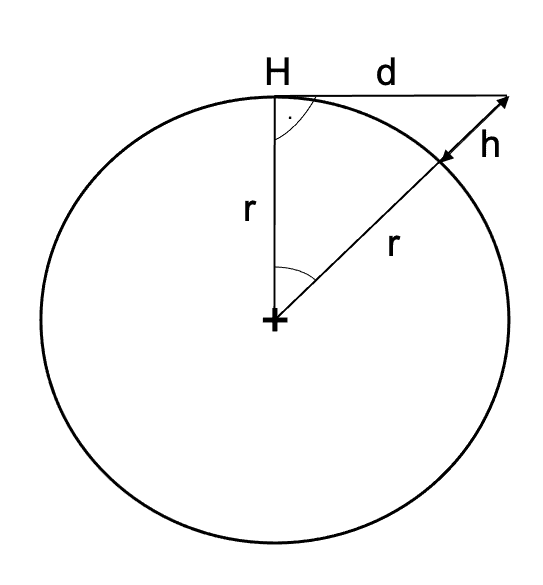
Obr. 1: Odvození vzorce pro výpočet vzdálenosti horizontu. d – vzdálenost horizontu H, r – poloměr Země (6 378 km), h – výška pozorovatele nad povrchem.
Samotný výpočet je pak jen přímé použití Pythagorovy věty. Vycházíme z obr. 1:
(r + h)2= d2 + r2
r2 + 2rh + h2 = d2 + r2
Postupně upravujeme:
d2 = 2rh + h2
d = √(2r + h)
Vzhledem k poměru velikosti h k velikosti poloměru Země r můžeme h v závorce zanedbat:
d = √(2r) = 2rh
Dosadíme za poloměr Země:
d = √(2hr) = √(2 × 6378 × h/1000) = 3,57√(h)
Výsledný vzorec pro výpočet vzdálenosti horizontu (v kilometrech) je:
d [km] = 3,57√(h)
My ale chceme zjistit, jaká by měla být vzdálenost mezi nejvyšším bodem v Haifě, hora Har Tlali = 480 m. n. m., a nejvyšším bodem na Krétě, hora Psiloritis = 2456 m. n. m., abychom je přes horizont viděli. Pozorujeme tedy objekt za horizontem tak, jak je ukázáno na obr. 2:

Obr. 2: Schéma výpočtu vzdálenosti objektu na horizontu.
K výpočtu jejich vzdálenosti použijeme vzorec odvozený výše, ale použijeme ho dvakrát. Celková vzdálenost mezi body d12 je dána součtem jednotlivých vzdáleností objektů k horizontu, tedy d12 = d1 + d2.
Dosadíme do rovnice a upravíme:
d = 3,57(√(h1) + √(h2)),
přičemž h1 je výška pozorovaného objektu na horizontu (Kréta, Ptilorilis) a h2 je výška, odkud pozorujeme (Haifa, Har Tlali).
d = 3,57(√(h1) + √(h2)) = 3,57(√(2456) + √(480)) = 255 km
Tedy z nejvyššího bodu v Haifě v Izraeli bychom viděli nejvyšší bod Kréty přes horizont jen tehdy, byly-li by tyto body vzdáleny méně než 255 km. Problém je, že letmá kontrola mapy odhalí, že tyto dva body jsou ve skutečnosti vzdáleny nějakých 980 km. To znamená, že ani ten nejdražší teleobjektiv není schopen z Haify vyfotografovat nejvyšší vrchol Kréty.
Můžeme ovšem vypočítat, jak vysoký by vrchol na Krétě musel být, abychom ho z Haify vyfotografovat mohli:
Pokud se díváme z hory Har Tlali, náš horizont bude ve vzdálenosti cca 78 km ( na tuto vzdálenost dohlédneme): d = 3,57√(h) = 3,57√(480) = 78,12 km.
Vzdálenost mezi Haifou a Krétou je 980 km, to znamená, že Kréta je ještě od horizontu vzdálena dalších 902 km (980 − 78). Nyní vypočteme výšku hory podle našeho vzorce, ze kterého nejprve musíme vyjádřit výšku h:
d = 3,57√(h) → h = (d/3,57)2
A dosadíme vzdálenost d:
h = (902/3,57)2 = 63 800 m ≈ 64 km
Tedy nejvyšší hora Kréty by musela vyrůst do úctyhodné výšky 64 km, a to už je pořádný kopec. Problém je, že takový se na Zemi žádný nenachází. Tak jen doufejme, že už jste se nevydali z úspor a nepořídili drahý teleobjektiv [2].
Pro Zeptej se vědce odpovídali Eliška a Vítek
Zdroje:
[1] Dotaz č. 839
[2] Skokan, L. (2003). Úvod do teorie geografie I, UJEP, Ústí nad Labem, ISBN 80-7044-482-7.
[3] Netopil R. a kol. (1984) Fyzická geografie. SPN, Praha.
[4] Brož, M., Šolc, M. (2013). Fyzika sluneční soustavy. Matfyzpress. ISBN 978-80-7378-236-8.
[5] Macháček M. (2004). Fyzika pro gymnázia – Astrofyzika. Prometheus. ISBN: 80-7196-277-5
[6] Armitage, P. J. (2020). Astrophysics of planet formation. Cambridge University Press.
[7] Široká, M., Bednařík, M. (2011) Fyzika pro gymnázia – Mechanika. Prometheus. ISBN: 978-80-7196-382-0
[8] Dotaz č. 949